Durante el desarrollo de mi tesis de maestría, me encontré con el reto de implementar una cola de prioridades en memoria externa (un modelo computacional distinto al convencional, del que hablaré en otra ocasión). En ese contexto, descubrí un artículo fascinante de Gonzalo Navarro y Rodrigo Paredes titulado "On Sorting, Heaps, and Minimum Spanning Trees", donde presentan una estructura llamada Quickheap.
¿Qué es Quickheap?
Quickheap se basa en una idea muy interesante: aprovechar el proceso de partición del algoritmo Quicksort, que tiene una complejidad promedio de 
para ordenar 
elementos. Sin embargo, en lugar de ordenar completamente, Navarro y Paredes proponen aplicar recursión solo sobre la mitad izquierda de la partición y registrar las posiciones de los pivotes seleccionados.
Una de las propiedades más llamativas de esta estructura es que los elementos entre dos pivotes consecutivos quedan delimitados en valor entre dichos pivotes, generando un orden parcial muy útil. Además, si un pivote ya no tiene elementos a su izquierda, ese pivote será el valor mínimo entre todos los elementos procesados.
Para garantizar siempre un pivote y un delimitador, se agrega un "infinito" a la derecha de todos los elementos iniciales, el cual actúa como primer pivote.
Aquí una imagen del proceso de construcción: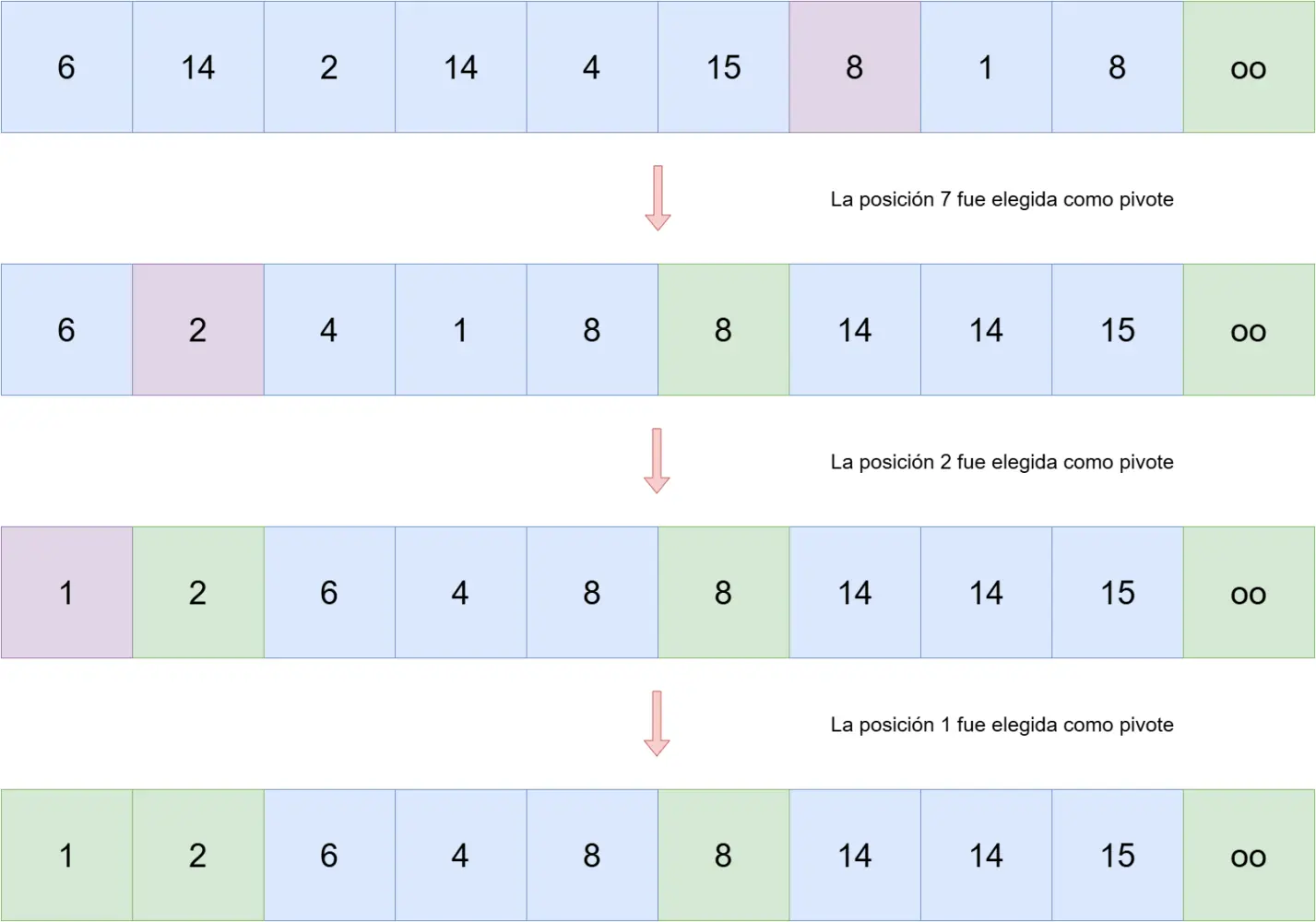
Propiedades destacables
Basado en el comportamiento del Quicksort, Quickheap hereda propiedades muy interesantes:
- El número esperado de pivotes es
. - Insertar elementos y extraer el mínimo veces toma .
- Las inserciones se pueden hacer en tiempo proporcional al número de pivotes.
- También permite:
Esto da lugar a una estructura eficiente, con operaciones logarítmicas en promedio y sin mucha complejidad adicional. Si quieren más detalles sobre la implementación (¡incluso en memoria externa!), les recomiendo leer el artículo original. Es una joya.
Evaluación práctica preliminar
Curioso por su rendimiento, decidí probar la estructura con algunos casos simples que solo requerían insertar elementos y extraer el mínimo, comparándola con std::priority_queue de C++.
Resultados preliminares: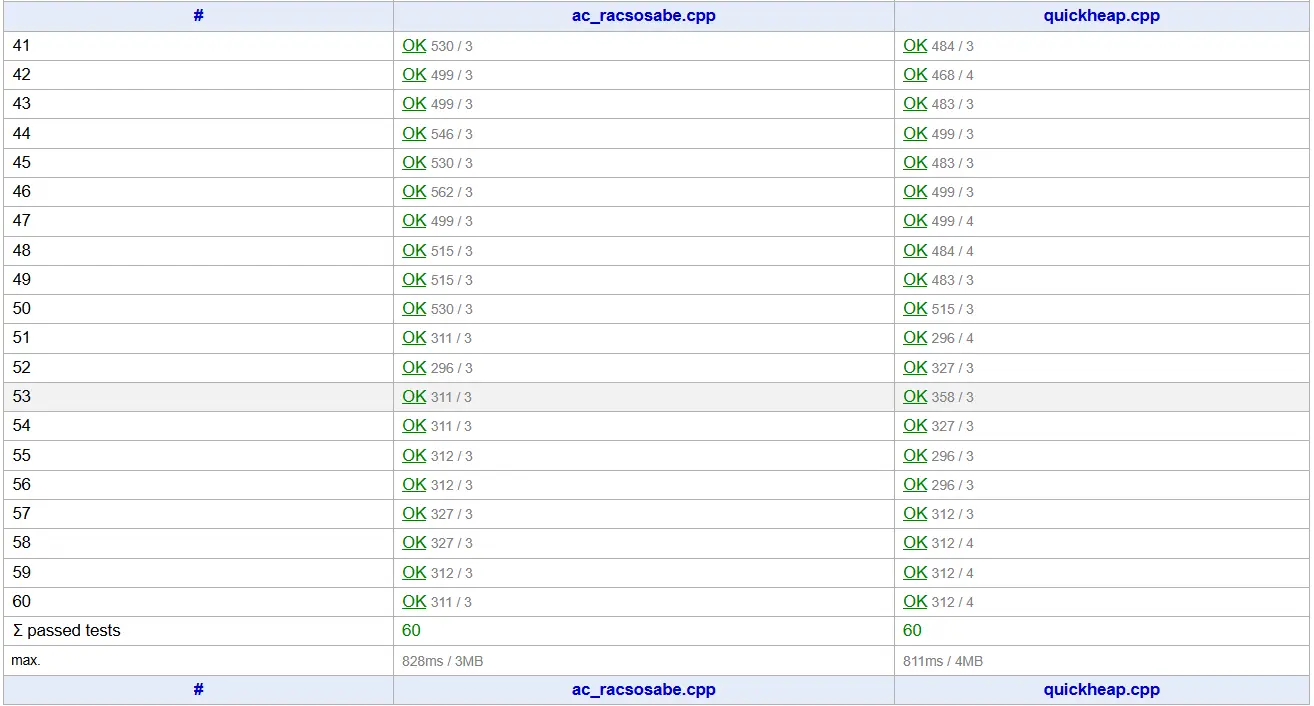
Nota: los tiempos de 828 ms y 811 ms no se muestran en la imagen, pero fueron tomados de los
primeros 40 casos.
Los resultados fueron alentadores: Quickheap se comportó de manera muy competitiva frente a la implementación nativa del STL.
Benchmark en un problema real: Jesse and Cookies
Probé varias variantes de Quickheap frente a std::priority_queue en un problema clásico de colas de prioridad. Aquí los resultados
Implementación Tiempo Memoria
STL Priority Queue 467 ms 12400 KB
Quickheap KV (mediana de 3) 468 ms 12000 KB
Quickheap KV (random pivot) 468 ms 12000 KB
Quickheap valor (mediana de 3) 437 ms 4200 KB
Quickheap valor (random pivot) 436 ms 4200 KB
El rendimiento promedio fue muy similar, ¡incluso Quickheap usó menos memoria!
Reflexión final
Mi conclusión principal: a veces, redescubrir un algoritmo clásico desde otra perspectiva puede llevarnos a diseñar nuevas estructuras de datos, tan competitivas como las herramientas más utilizadas hoy en día. Nunca habría imaginado que una variación tan simple sobre Quicksort podría derivar en una alternativa eficiente a los heaps. A partir de ahora, intentaré mantener la mente más abierta para este tipo de ideas.
Estudiante Maestría UNICAMP
Mundialista ICPC
Quickheap: una alternativa ingeniosa basada en Quicksort