IEEE 754 y lo que todo programador debe conocer

Historia

Imagina un laboratorio de la era de los mainframes, donde ingenieros y científicos luchan por trasladar sus cálculos entre máquinas incompatibles. En los años 1960 y 1970, cada fabricante—desde IBM con su formato hexadecimal de punto flotante hasta CDC y Cray con representaciones en complemento a uno—ofrecía su propia versión de cómo manejar mantisas, exponentes y excepciones como división por cero, incluso permitiendo +0 y -0 como valores distintos. La comunidad inventaba trucos extraños en los programas para evitar resultados aberrantes y hacía que el software numérico portable fuera cada vez más costoso e inaccesible para la mayoría de desarrolladores. Bajo este panorama, John Palmer en Intel y William Kahan en Berkeley comenzaron a advertir que, sin un estándar global, el progreso de la computación científica estaba en riesgo: las empresas gastaron fortunas en verificar y retocar código para máquinas específicas, en lugar de centrarse en la innovación.A finales de los 70 y principios de los 80 surgió la propuesta que desembocó en IEEE 754-1985, impulsada por William Kahan y comités de IEEE con retroalimentación de la industria, definiendo formatos binarios, NaN, ±∞, reglas de redondeo y manejo uniforme de excepciones. Aunque con variantes y nuevas versiones —2008, 2019 y futuras revisiones— este estándar sigue siendo la base de la computación numérica moderna, garantizando que un mismo algoritmo produzca resultados predecibles sin importar la arquitectura subyacente.


William (Velvel) Morton Kahan
 

Representación por bits

Cada número se presenta por un “código secreto” de bits, que revela su signo, magnitud y alcance. En IEEE 754, este código está dividido en tres campos: un bit de signo (0 para positivo, 1 para negativo), un campo de exponente con sesgo (bias) que permite abarcar exponentes positivos y negativos, y una fracción o mantisa normalizada que contiene los bits significativos del número. Gracias al sesgo en el exponente, se puede representar tanto valores muy pequeños como muy grandes dentro de un espacio de bits fijo; además, se reservan patrones especiales de bits para ±0, ±∞ y NaN (Not-a-Number) que indican casos excepcionales. Las representaciones “subnormales” cubren el rango inmediato alrededor de cero, garantizando continuidad en los valores muy cercanos a cero. Esta estructura uniforme en todos los procesadores facilita el traslado de datos numéricos entre sistemas sin ambigüedad en su interpretación.

Ejemplo:

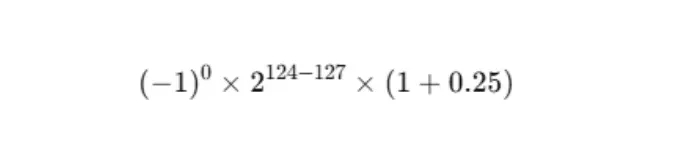
Operaciones con bits

Cuando el hardware recibe una operación (suma, resta, multiplicación o división), sigue un protocolo estricto para alinear y procesar los operandos dentro de los campos de exponente y mantisa. Por ejemplo, en la suma: primero “alinea” los exponentes desplazando la mantisa del operando de menor exponente, luego suma o resta las mantisas, normaliza el resultado (ajustando el exponente si es necesario) y finalmente aplica la regla de redondeo establecida (como “al más cercano, con empate al par”). Multiplicaciones y divisiones combinan exponentes y operan sobre mantisas antes de normalizar y redondear. Cada paso busca maximizar la precisión dentro de la cantidad limitada de bits, pero siempre hay pérdidas inevitables. El estándar define también cinco excepciones con sus banderas:

• Inválido
• División por cero
• Desbordamiento (overflow)
• Subdesbordamiento (underflow)
• Inexactitud (inexact)

De modo que si un cálculo sale de rango o no puede representarse exactamente, se levanta la bandera correspondiente y se genera ±∞, un subnormal o NaN según el caso, permitiendo a software y sistema operativo detectar y manejar estas señales.

La mediana de los números flotantes es 1.5

Aun así, esta estructura tiene curiosidades anti-intuitivas. Imaginemos que queremos saber cuál es el punto medio de todos los números positivos finitos que puede representar la computadora: en un primer razonado podríamos pensar que ese número es muy grande, quizá la mitad del máximo representable (por ejemplo, la mitad del float máximo ≈3.4·10^38/2 ≈1.7·10^38), o cercano a él. Muy por lo contrario, al formular y resolver el problema, resulta más sorprendente: la mediana de todos los floats positivos finitos es 1.5:




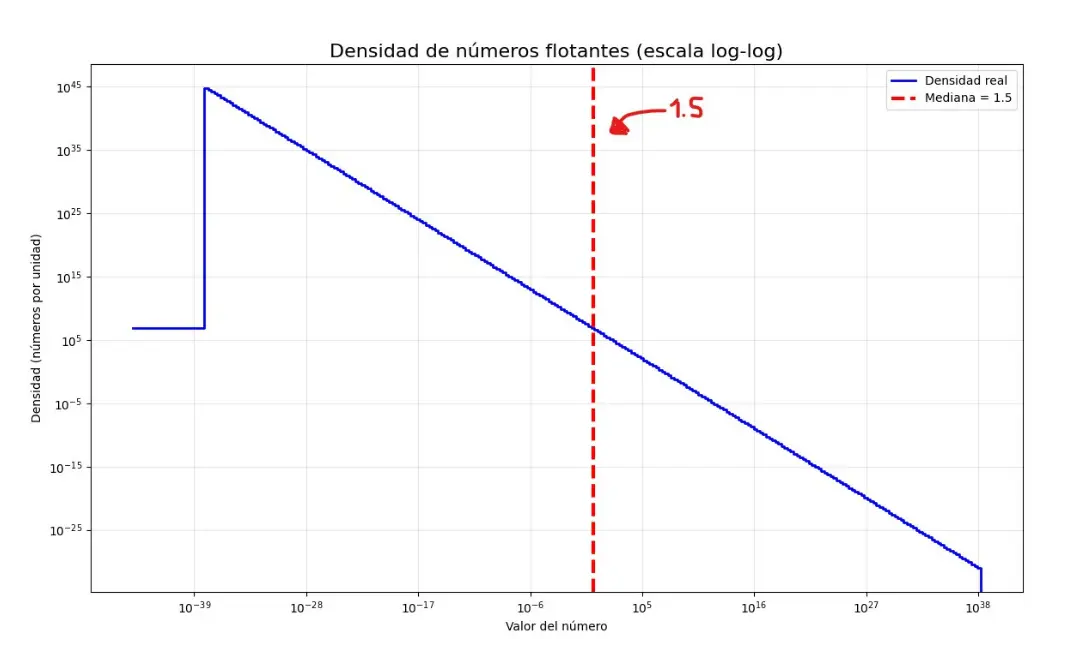
figura 1. Gráfica de la densidad de los números float32

Este resultado nos dice que, al ordenar todo el espacio finito de representaciones de floats positivos, la mitad cae por debajo de 1.5 y la otra mitad por encima (véase figura 1). En la práctica, sugiere que trabajar con magnitudes cercanas a 1 minimiza el crecimiento del error absoluto (véase figura 2) , dado que el espaciamiento entre valores representables aumenta con el exponente. Por ello, en gráficos y simulaciones se normalizan vectores a longitud 1 para mantener los cálculos en rangos moderados y evitar overflow o underflow; Sin embargo, debido a cómo el estándar maneja el error, este es predecible y confiable al trabajar con distribuciones y cálculos estadísticos.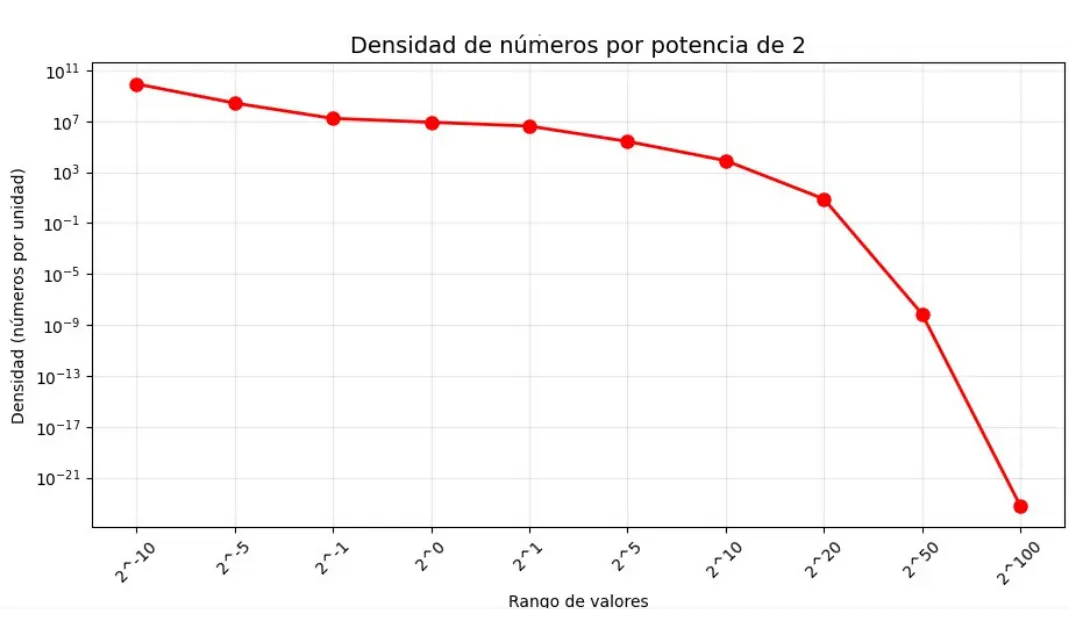

figura 2. Gráfica de la densidad de los números por precisión

Técnicas para Evitar la Pérdida de Precisión

1. Normalización de Vectores





2. Comparaciones y Restas Estables



3. Técnicas de Suma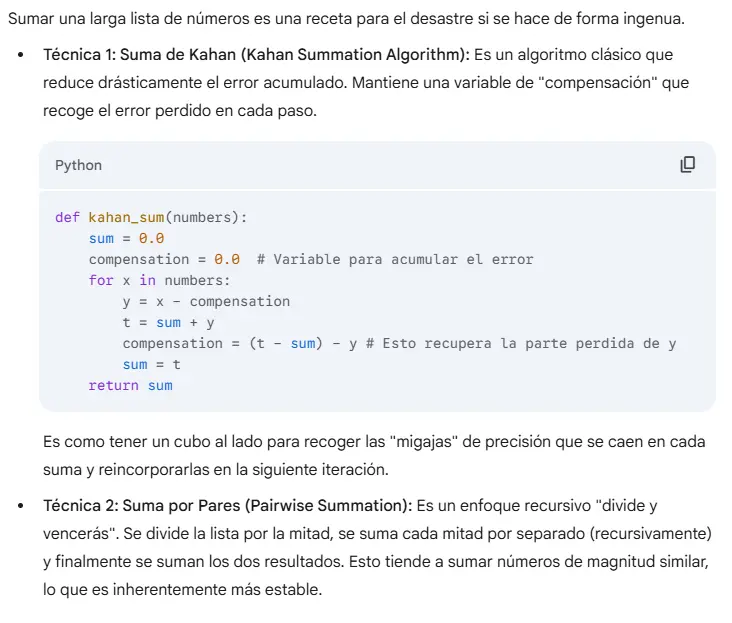

Conclusión

Los números de punto flotante no son reales perfectos, aunque muchas veces lo parezcan. Son una forma limitada, pero muy ingeniosa, de representar decimales en una computadora. Nos permiten trabajar con escalas enormes o muy pequeñas, pero siempre con un margen de error.

Aun con sus imperfecciones, el punto flotante representa uno de los mejores esfuerzos que hemos desarrollado para acercarnos al mundo continuo de los números reales desde una máquina digital. No es exacto, pero cuando se usa con conocimiento, es sorprendentemente confiable.

Miguel Alessandro Mini Huambachano

Estudiante PhD UNICAMP

Mundialista ICPC