La operación más simple que existe cuando trabajamos con cadenas de caracteres es comparar un par de cadenas. Es cierto que este proceso naturalmente puede ser lento dependiendo del escenario, pero en algunos de ellos se pueden realizar procedimientos mucho más eficientes.
Sentando las bases
Toda cadena es una secuencia de caracteres que pertenecen a un conjunto llamado alfabeto, el cual está ordenado de alguna forma (para los dígitos por comparación, para las letras por ubicación, etc.). Ya que el alfabeto define un orden sobre los caracteres, es natural definir un orden sobre cada secuencia de estos: el orden más usado es el llamado lexicográfico
El orden lexicográfico define la relación entre una cadena S y una cadena T tomando como referencia los siguientes escenarios:
- Si S es igual a T, entonces son iguales y no se establece una relación estricta entre ellos. Por ejemplo, "hola" es igual a "hola", naturalmente.
- Si S es un prefijo propio de T, entonces S es menor lexicográficamente que T. Por ejemplo, "abra" es menor lexicográficamente que "abracadabra".
- Si T es un prefijo propio de S, entonces S es mayor lexicográficamente que T. Por ejemplo, "patineta" es mayor lexicográficamente que "patin".
- Si i es la primera posición tal que S[i] es diferente a T[i], entonces S[i] aparece antes que T[i] en el alfabeto usado. Por ejemplo, "casa" es menor lexicográficamente que "caso" porque la letra a aparece antes que la letra o en el alfabeto.
De esta manera, podemos decir que las siguiente relaciones serían correctas en un contexto de cadenas:
- "abc" < "abcd"
- "hola" > "adios"
- "124" < "1230"
- "123" < "hola"
Hasta el tercer ejemplo todo está bastante claro, pero ¿Qué significa que "123" sea menor que "hola"? Esta pregunta la responde el famoso código ASCII.
Código ASCII
El código ASCII nace con la finalidad de asociar un caracter a un número entero de 7 bits, de manera que se podría representar 128 caracteres posibles usando este método. Naturalmente, este comenzó a ser utilizado y extendido en algunos lenguajes y sistemas de programación volviéndose un estándar.
La asociación de un caracter a un número permite una mayor flexibilidad al momento de realizar comparaciones en general, ya que el alfabeto ya no solamente serían las letras sino también incluiría los números e incluso símbolos matemáticos, entre otros. Es debido a ello que, como se ve en el ejemplo anterior, "123" es menor que "hola", ya que las secuencias traducidas a enteros (según ASCII) serían:
- (49, 50, 51) < (104, 111, 108, 97)
Ahora que entendemos cómo es que se comparan los caracteres de una cadena, veamos cómo se pueden comparar cadenas eficientemente según algunos escenarios.
Escenario 1: 1 vs 1
Cuando nos encontramos en un escenario en el cual solo tenemos que comparar las cadenas S y T una única vez y estas pueden ser aleatorias, no podemos hacer nada más que compararlas directamente, es decir, realizar un bucle hasta que se cumpla alguno de los escenarios previamente señalados.
Es sencillo notar que la complejidad de este algoritmo será de O(min(|S|, |T|)), lo cual no es tan malo en términos generales.
Escenario 2: 1 vs n
Ahora consideremos un caso en el que tenemos una sola cadena S y n cadenas T[i] con las cuales queremos compararlas, es decir, S vs T[0], S vs T[1], etc.
Es cierto que podríamos aplicar el método anterior y obtendríamos una complejidad de O(min(|S|, |T[0]|) + min(|S|, |T[1]|) + ... + min(|S|, |T[n - 1]|)), lo cual podría llevarnos un tiempo considerable pero prudente.
Escenario especial: S vs S'
Finalmente, consideremos un caso en el que deseamos comparar una subcadena de S con otra subcadena de S, por ejemplo, si S = "abracadabra" y queremos comparar S[1, 4] = "brac" con S[7, 10] = "abra", ¿Qué deberíamos hacer para evitar una complejidad de O(|S|)?
Tenemos dos posibilidades para esto.
Hashing polinomial
El hashing polinomial considera a cada cadena como si estuviera en una base B, donde B debe ser mayor que el valor numérico de cualquier caracter en la cadena (incluso es sencillo notar que se puede remapear cada caracter a un valor entre 0 y |S| - 1). En un caso ideal con una aritmética ilimitada, podríamos calcular dicho valor sin problemas, pero en la realidad no tenemos tanta capacidad de maniobra. Lo anterior nos dice que deberíamos tener una función f(S) que no tenga un valor tan grande pero al mismo tiempo tenga cierto margen de error previsible.
La respuesta más simple a dicha problemática es tomar el valor del polinomio pero módulo un entero m, de manera que O(|S| / m) será nuestra probabilidad de error dado que la base B sea coprima con m (esto es sencillo de lograr si m es un primo directamente). Hay mucha más teoría detras del hashing polinomial pero eso no es de mucho interés por el momento, nos basta con saber la idea base de la técnica.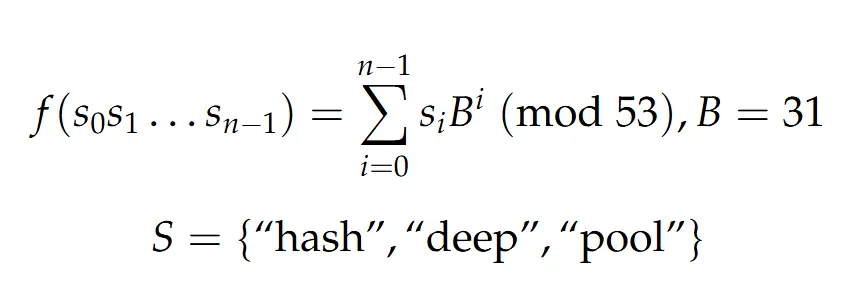
Entonces, ¿Cómo comparamos las subcadenas? Podemos calcular las prefix sums P del polinomio de manera que un rango [a, b] se puede calcular en base a P(b) - P(a - 1); sin embargo, al ser un polinomio, es posible que las dos subcadenas a comparar empiecen en una posición diferente (por lo tanto, estarían siendo multiplicadas por una potencia de B diferente) así que tendremos que emparejarlas multiplicando por la potencia de B correspondiente.
Lastimosamente, este método solo nos sirve para comparar igualdad en tiempo O(1), mientras que es posible usar búsqueda binaria con dicha comparación de igualdad para comparar lexicográficamente en O(log|S|). Es importante recordar que este método es probabilístico, así que no siempre va a dar una comparación correcta.
Sparse Table + Compresión
Otra alternativa que tal vez no es muy recurrente es la de usar Sparse Table, la cual es una estructura que calcula información de rangos que tengan un tamaño que sea una potencia de 2, de manera que tendría solo O(log|S|) niveles de tamaño O(|S|) cada uno. Este método parte de comprimir los caracteres de manera individual (Nivel 0), luego para el siguiente nivel se formarán pares (x, y) que corresponden a los dos caracteres que forman la cadena de tamaño 2 en cada posición, en el siguiente nivel se formarán nuevos pares que ahora representarán a cadenas de tamaño 4 y así hasta que ya no se pueda formar cadenas con longitud válida.
Es posible construir toda la tabla en O(|S|log|S|) usando counting sort para ordenar los pares y luego asignarles el mapeo correspondiente.
Considerando que ya se tiene la tabla construida, se puede comparar dos subcadenas de mismo tamaño mediante el siguiente algoritmo:
Donde no es tan evidente notar que la comparación de dichos pares coincide con la comparación lexicográfica pero se puede argumentar analizando donde estaría la posición del primer caracter que difiere.
La desventaja de este método es que la construcción toma O(nlogn) pero la consulta toma O(1) sin margen de error (es decir, siempre da la comparación correcta).
Y bueno, esto es todo por el momento, puede que vuelva a escribir un nuevo artículo sobre búsqueda de patrones o algunos algoritmos sobre cadenas próximamente, así que estén atentos a nuestras redes sociales.
Estudiante Maestría UNICAMP
Mundialista ICPC
¿"123" < "hola"? Entendiendo comparaciones entre strings